Some more examples we prepared earlier ...
No morphology or patterning is imposed on the cyberhyphal community as it develops by the Neighbour-Sensing mathematical model; the patterns which do emerge in the growth of cyberfungi, in the computerspeak of the day, are unscripted. They are the natural outcome of the growth mechanisms programmed into the model, and those growth mechanisms are specifically characteristic of live, real-world fungi.
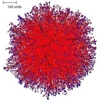
It is significant, therefore, that a spherical colony is formed under conditions when all growth regulation is turned off (so that branching occurs at random times and new branches grow in random directions. This is illustrated in Figure 1, below. Such simulations produce relatively solid tissues. The slice command allows investigation of the internal structure of these tissues. The slice of the colony in Figure 1 shows that the colony is much denser in the centre than at the boundary.
| Figure 1. The spherical colony formed when parameters are set for branching at random times, with new branches growing in random directions. The external view of the mycelium is shown at left (the red colour in the figure indicates growing and branching tips, and the central slice is shown on the right. | |
A spherical colony is also formed when branching is set to be sensitive to the quantity of hyphal tips in the neighbourhood; and illustrated in Figure 2.
|
|
|
| Figure 2. The spherical colony formed when parameters are set to make branching sensitive to the number of hyphal tips in the neighbourhood. In this simulation, growing and branching tips are colour-coded red, tips that are not branching in this iteration of the algorithm (because the population in their local environment is too dense to permit branching) are colour-coded blue. | |
With branching set to be regulated by the hyphal density field a spherical colony is again formed. This tropic field is described using physical laws derived from the properties of electric fields, and produces the most regular colony shape, but the slice shows that it, too, contains a high hyphal population density zone in the centre (Figure 3).
| Figure 3. The spherical colony formed when parameters are set to make branching sensitive to the hyphal density field. In this illustration, growing and branching tips are colour-coded red, tips that were not eligible to branch in this iteration because of a too dense hyphal density field environment are colour-coded blue. | |
It may not be too surprising that allowing growth and branching from the initial central point of these simulations results in ‘solid’ spherical mycelia, but some surprises did emerge from these experiments!
Applying the rule that both negative autotropism and branching should be based on the hyphal density field also produced a regular spherical colony, but the internal structure (see slice below) was markedly radial (Figure 4).
| Figure 4. The spherical colony formed when parameters were set so that both negative autotropism and branching were based on the hyphal density field. | |
Another interesting example is the spherical colony formed using negative autotropism but setting branching to be regulated by the number of neighbouring tips (not by the density field)(Figure 5). This colony morphology was much more 'open' and the colony margin was ragged.
| Figure 5. The spherical colony formed using negative autotropism but setting branching to be regulated by the number of neighbouring tips. Again, growing and branching tips are red, tips that are not eligible to branch are blue. | |
During the early stages of development of a colony such as is shown in Figure 5, a curious and unexpected feature emerged: the hyphae differentiated into two morphological classes. There were hyphae that grew from the centre directly to the outer border, and those that filled the rest of the space. This feature was most clearly evident at early stages in the simulation (Figure 6).
| Figure 6. Early stage mycelium formed by a parameter set using negative autotropism but setting branching to be regulated by the number of neighbouring tips. Growing and branching tips are flagged red, tips that do not branch due to a too dense environment are flagged blue. |
It is important to stress that the parameter set used for Figures 5 & 6 does not specify that there will be the two types of hyphae! They emerge as a natural outcome of the operation of a parameter set applied initially to one hyphal type. This branching model corresponds to the Amanita rubescens default parameter set described on an earlier page [view now] and it would be interesting to experiment further with this parameter set to establish why and how the two hyphal types differentiate.
However, this experiment led us to add several enhancements to the model that enabled hyphae in simulations to differentiate. Experiments done with these enhancements are illustrated below.
The original model dealt with only one sort of hypha, but we decided to enhance this by offering three categories of hypha:
- standard hyphae are those that normally start developing when a simulation is initiated;
- leading hyphae can emerge from the colony peripheral growth zone (with a probability determined by the user) to take on a leading role (in the formation of cords, as explored below, for example); and
- secondary hyphae are branches that arise late, far behind the peripheral growth zone, when mature hyphal segments (of either standard or leading hyphae) resume branching to infill the older parts of the colony.
All hyphal types can be made sensitive to the full range of growth vector regulation, and can be given parameter sets that are different from the other hyphae used in a simulation. The user can also determine the probability that a new branch will become a leading or secondary hypha.
Mathematically the different categories of hyphae are implemented as additional objects, and the JavaTM program is expanded to provide user interfaces so that parameters can be set individually for each sort of hypha.
We also introduced a horizontal plane tropism that provides a way of simulating colonies growing in or on a substratum like agar or soil by imposing a horizontal constraint on the data space the cyberhyphal tips can explore. The effects of this are illustrated in Figure 7.
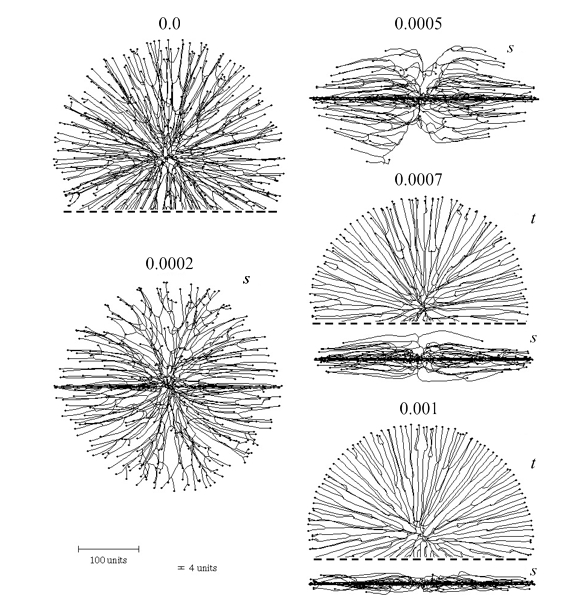 |
| Figure 7. Effect of the horizontal plane tropism on the shape of the colony. The numbers above the images indicate the selected impact factor (= ‘strength’) of the horizontal tropism constant (HTC). With an impact factor of zero the colony is spherical. The thickness of the ‘horizontal zone’ was set to 4 distance units (see scale bars at bottom left). For some of the symmetrical shapes only part of the view is shown, the dashed line indicating where the image has been cropped. Two viewing angles are shown, s = side view, t = top view. The growth was simulated assuming negative autotropic reaction (persistence factor = 0.1) and density-field dependent branching (threshold 0.06), with the density field being generated by all of the mycelium (lc = 20). If the density allowed branching, the branching probability was 40% per iteration (per time unit). The age of all colonies shown is 220 time units. |
The secondary hypha routine enables the emergence of structures from a colony to be modelled. For example, imposing secondary branching on a flat colony formed using the horizontal plane tropism, but releasing the secondary branches from the horizontal plane tropism and making them negatively gravitropic instead, results in emergence of randomly distributed bundles of hyphae (the mycological term would be ‘fascicles’) growing up from the colony, rather like sporing structures emerging from a Petri dish culture (Figure 8). The result of combining the horizontal plane tropism with hyphal differentiation is a superbly realistic ‘Petri-dish mycelium’ (Figure 8, which also illustrates how the cybermycelium can be rotated in the data space to change the viewing aspect).
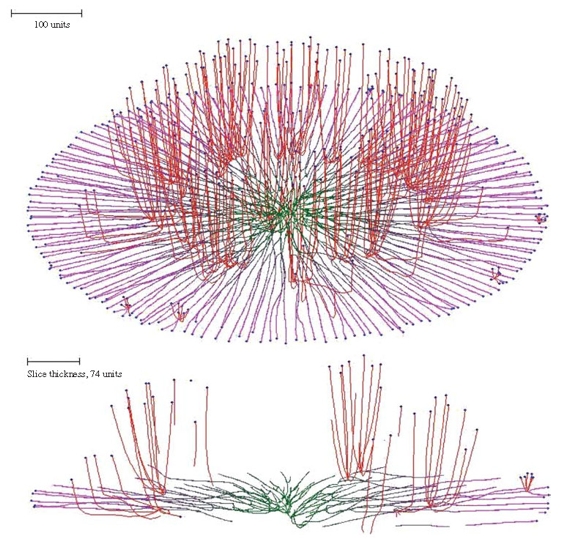 |
| Figure 8. Oblique view and slice of a mycelium grown under the influence of the horizontal plane tropism and in which secondary branching was activated at the 220 time unit. Differently from the primary hyphal branches (subjected to the horizontal tropism with an impact constant of 0.0007, and zone height of 4 distance units), the secondary branches had a negative gravitropism imposed (impact constant 0.002). For both primary and secondary hyphal branches the growth was simulated assuming negative autotropism (persistence factor k = 0.1) and density-dependent branching. The branching threshold was 0.06 at the apex and 0.12 at the old branch points forming secondary branches (maximum 8 new branches per branch point). The density field was generated by the whole mycelium (lc = 20). If the density allowed branching, the branching probability was 40% per iteration (per time unit). The final age of the colony shown was 294 time units. Secondary branches are colour-coded red, and hyphae of the primary mycelium are coloured green (oldest) to magenta (youngest), depending on the distance of the hyphal segment from the centre of the colony. |
Remember that the program generates its structures by creating and plotting individual hyphal tips. All the visualizations we illustrate are made up of hyphal tips, sometimes many thousands, which are expressing independently the growth rules that have been assigned to them.
Users who wish to inspect the detail of hyphal tip behaviour can zoom into the simulation to do so. The detail can be ignored by zooming out to view overall morphology. The detail can be changed by altering the parameters.
Where hyphal tips are interacting with other hyphae, the trajectory of a hyphal tip that is approaching another hypha under the infuence of an autotropism strongly depends on the angle of approach. Alleviation of the negative autotropism causes hyphal aggregation of secondary hyphae but is very sensitive to the branching angle. At acute approach angles, tips curl in a manner that may cause the approaching hyphal tip to curl around its target in a spiral; in contrast an obtuse angle results in the approaching tip ‘orbiting’ its target aimlessly.
Although this results in hyphal aggregation, it is not sufficient to cause formation of more ordered linear structures such as stands, cords and rhizomorphs, so the overall pattern of mycelia generated under these conditions is very different from the known morphology of real mycelia producing cords. On the other hand, this sort of behaviour is rather reminiscent of tendril hyphae and, more generally, of the ‘hyphal knots’, in which a central inducing hypha is thought to cause a concerted pattern of differentiation in a surrounding family of other hyphae [learn more about this elsewhere on this website in Chapter 12: Development and morphogenesis of our 21st Century Guidebook to Fungi, especially section 12.16].
Fungi form several linear structures which consist of many hyphae growing in parallel in the same direction; they are given names like strands, cords, rhizomorphs, mushroom stems. Models based only on combinations of negative and positive autotropisms cannot effectively simulate the morphogenesis of such structures because strong positive autotropism (needed to bring the hyphae together) tends to turn the hyphae towards the centre of the mycelium, and because approaching hyphae have no reason to turn to grow in the same direction.
Observations on cord formation between a bait and an inoculum by mycelia of the fungus Phanerochaete velutina shows that hyphae do indeed grow in both directions, so there seems to be some tolerance of a certain amount of uncertainty in vivo. However, the mathematical model requires a solution that does achieve concerted growth of linear structures and an approach that is successful in this is implementation of an orientation field.
The (mathematical) features required of an orientation field capable of forming linear structures are that it must be a vector field with direction running parallel to the direction of the linear structure we wish to create. Implementing a galvanotropism into the model solved this problem. From the literature it was evident that bacteria and fungi alike exhibit tropisms to electric fields and currents. Further, differentially-distributed ion pumps produce ionic currents that leave the growing hyphal apex and re-enter the hypha at more basal regions.
Hence, at least in some regions the lines of force of the corresponding electric field may be close to parallel to the hyphal axis of living fungi. Such a field has the required directionality that can be used for orientation.
Because the lines of force of the field from each hypha are oriented in the same direction the shared field of any linear structure that is formed can be much stronger than a single hypha is able to generate. Hyphal recruitment to a developing cord will be a self-accelerating process.
We wish to stress that although an electric field seems a likely candidate for this particular tropism (and we refer to it as a galvanotropism), the mathematical model employs an abstract definition of the orientation field that is not dependent on any particular mechanism of generation and/or perception. Other mechanistic hypotheses are not excluded providing they can generate a directional field parallel to the hyphal long axis.
The specific features of this galvanotropism as implemented in the program result from the assumption that each hyphal segment, short enough to be considered as a straight line, forms an orientation field directed toward the end that is closer to the segment’s hyphal tip and is parallel to the hyphal long axis.
The absolute value of the field at any given point is inversely proportional to the shortest distance from that point to the segment generating the field. The total field of a mycelium perceived at any given point is a vector sum of the fields generated by all such mycelial segments.
Implementing this feature in the Neighbour-Sensing model is sufficient to switch the morphology of the simulation from a diffuse spreading fan-like mycelium to a mycelium forming aggregated structures similar to strands and cords (Figure 9).
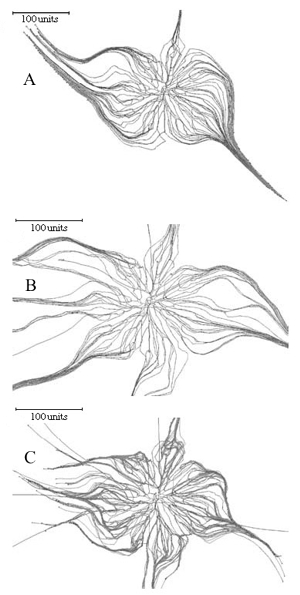 |
Figure 9. Using the galvanotropic reaction to develop mycelial strands and cords. Figure 9A: the initial colony was grown for 98 time units with a parameter set that included negative autotropism, a tropism persistence factor of 0.1, density field-regulated branching (with a threshold of 0.06), probability of branching of 40% per time unit, growth rate proportional to length (proportionality coefficient 0.1, maximum 5 length units per time unit), density field generated by all of the mycelium. A horizontal plane tropism was implemented to limit the hyphal tips to a horizontal layer with a thickness of 40 standard distance units. After the 98 time units, the galvanotropism was activated (impact factor 0.1) together with the corresponding positive tropism (impact factor 0.15). Figure 9B: development of cords using leading hyphae. Probability of the new branch becoming a leading hypha was set to 10%. Leading branches (colour-coded blue) lack galvanotropic sensitivity; other parameters as for Figure 9A. Figure 9C: development of cords with leading branches and allowing secondary branching (so that cords can arise from within the mature regions of the colony). The density field threshold for secondary branching was 4 times higher than that set for standard or leading hyphae. Other parameters were identical to those used for the simulation in Figure 9B. |
Figure 9A shows that the basic model does not require any additional assumptions to generate cords analogous to those formed by such fungi as Phanerochaete in vivo. There is a considerable amount of evidence to indicate that in real mycelia leading hyphae can organise cord formation around themselves, and cords can be formed from within the mature regions of a colony. Introducing the concepts of leading and secondary hyphae into the program enables simulation of these circumstances. If leading hyphae in the simulation are set to lack the galvanotropic response they do not join cords that are being formed, but instead become the initiating centres for more cord formation (Figure 9B).
Secondary branches are initiated at previous branch points if the local density is below the branching threshold set by the user. Mycelia formed by growing and branching of standard hyphae are usually dense enough to suppress secondary branching, so the model supports an additional constant that enables the user to define a difference in value between the critical hyphal density field controlling standard and secondary branching.
Adding secondary branching to the cord-forming parameter set produces a colony that forms cords from both the peripheral and central regions (Figure 9C).
The Neighbour-Sensing model can generate quite realistic strand-like and cord-like structures, but they dominate the mycelium in an unrealistic fashion. We believe that the key to the low level of visual similarity is most probably the number of hyphal tips involved in the simulation. There must be many thousands of hyphal tips in the live cultures, but impressive computing power is required to simulate this.
The pattern of growth of all hyphae can be influenced in a localised manner by placing ‘substrates’ in the growth space. The cybermycelium in Figure 10 (below) was grown using negative gravitropism implemented at -20º, but two spheres of an attractive substrate (green) and one of an inhibitory substrate (red at centre) were also added to modify the growth pattern.
The slice taken through the vertical centre shows the tips growing around the inhibitory substrate and towards the attractive substrates. Once inside the sphere of influence of the attractive substrates the tips are unable to free themselves until the user removes the substrates from the growth space.
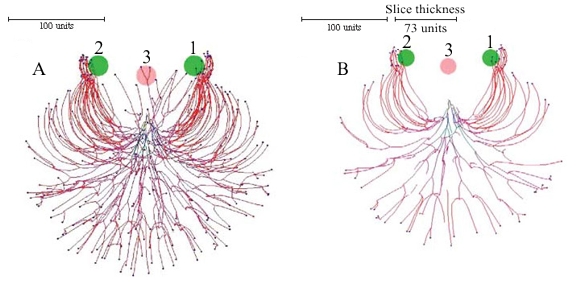 |
| Figure 10. Inserting substrates and inhibitors into the data space. The growth was simulated using negative autotropic reaction (persistence factor k = 0.1) and density field dependent branching (threshold 0.06), with the density field generated by all of the mycelium (lc = 20). If the density allowed branching, the branching probability was 40% per iteration (per time unit). Two spheres of attractive (green, and labelled with numerals 1 and 2), and one inhibitory (red, labelled 3) substrates were added to modify the growth pattern further. The field generated by substrates is 1000 times stronger than the field generated by a mycelial segment with a length equal to 20 distance units. The coordinates in the data space of the attractive substrates was (50, 0, -50) and (-50, 0, 50), the inhibitory substrate was placed at (0, 0, -40). The radius of all substrates was 20 (all values are given in program distance units). Fig. 10A is a view of the whole (three dimensional) mycelium, and Fig. 10B is a slice through the centre of the object showing how the hyphal tips have avoided the inhibitory substrate and congregated around the attractive ones (tips which appear to be within the inhibitory substrate in Fig. 10A are situated above the substrate). Colour of a hyphal segment in these figures depends on the number of growing tips the segment supports, from black (supporting many tips) to red (one tip). |
One of the first surprises to arise from our experiments with long-running simulations resulted from the application of a gravitropism field to a simulation started off with the default parameters known as the Tricholoma type. Causing the tips to try to grow at a 45 degree angle in relation to the orientation (gravitropism) field not surprisingly produces a conical or cup-shaped structure (Figure 11).
| Figure 11. The conical mycelial mass resulting from the application of a gravitropism field to a simulation causing the tips to try to grow at a 45 degree angle. |
The slice illustrated in Figure 12 shows that the mycelium forms a hollow cone, but the most unexpected outcome of this simulation is that the slice shows that voids or 'locules' are formed within the tissue of the cup-shaped structure (Figure 12).
| Figure 12. Internal structure of the conical mycelium shown in Figure 11. Note that the conical structure is not only hollow, but has a series of voids or ‘locules’ within the tissue towards the base of the cup. |
So there's another set of in silico experiments that need to be done! What is it about this combination of control parameters that leads to the formation of voids? How can the morphology, size, number and distribution of the voids be controlled? And what might all that tell you about the way that real live fungi control the internal structures their fruit bodies?
Please remember that although we call this a gravitropism, in terms of the mathematics of the model it is simply an orientation field around the vertical axis. In physiological terms it could be gravity, but it could equally well be incident illumination, a temperature gradient or a chemical gradient. That's up to you to define.
More aspects of the implementation of the gravitropism field were explored in experiments illustrated in Figure 13.
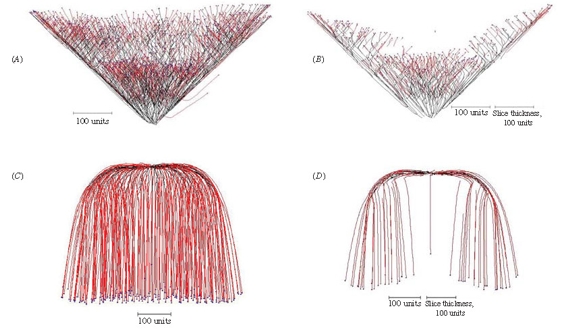 |
| Figure 13. Implementing the gravitropic response. (A) Setting the angle of gravitropism to -45º produces a cone-shaped structure. (B) A slice through the centre of the cone shows that it is a hollow cup-shape; this is a consequence of negative autotropism, which has a stronger effect in the crowded central region and forces the new tips to grow away from the central axis. (C) Implementing root-distance-dependent gravitropic angle turn gradually changes the angle of gravitropism from one value to another over the course of a (user-)defined distance between the tips and their ‘roots’ (equivalent to branch length). In this example, the angle of gravitropism starts at 90º and when the length of the branches reached 100 length units the angle of gravitropism was gradually turned towards 180º, reaching this value when the branch length was 500 length units. (D) A slice through the centre of 13C shows that the negative autotropism, which was also implemented, has forced the growing tips away from each other as they grew towards the bottom of the structure. |
When gravitropism is implemented a vector is added to each hyphal tip corresponding to the angle of gravitropism set by the user and for positive angles the tips are constrained to grow downwards in the user’s field of view.
If the angle of negative gravitropism is set to -45º a cone-shaped structure is produced as the tips are constrained to grow upwards (Figure 13A), but a slice through the centre of this shows that it is a hollow cup-shaped structure rather than a solid cone (Figure 13B). This is a consequence of negative autotropism being implemented as well, which has a stronger effect in the crowded central region and forces the new tips to grow at 45º away from the central axis.
This observation of a structure with similarities to a cup-fungus fruit body suggests that a combination of relatively simple tropisms may be able to generate simulations of other fungal fruit bodies. By implementing gradual rotational adjustment of the gravitropic angle in a manner that is dependent on branch length it is possible to generate smoothly curved structures.
In the example shown in Figure 13C, the angle of gravitropism was started at 90º and when the length of each branch reached 100 length units the angle of (positive) gravitropism was gradually turned towards 180º, reaching this value when the branch length was 500 length units. A slice through the centre of this visualization (Figure 13D) shows that the hyphal tips were forced away from each other and towards the outer and bottom margins of the structure because negative autotropism was also implemented.
For the structure shown in Figure 14, a long-range positive autotropism was implemented as well as negative autotropism and negative gravitropism (-45º). Whereas the strength of the negative autotropism vector is quite localised (because it attenuates at a rate inversely proportional to the square of distance), the long-range positive autotropism vector is effective over longer distances, being inversely proportional to the square root of the distance.
In this example, the mycelium developed as it would without the long range positive autotropism to form the basal part of the structure, until the tips reached a threshold distance from the main bulk of the mycelium when they were directed back towards each other and a closed structure resulted.
 |
| Figure 14. Combining long-range positive autotropism, negative autotropism and negative gravitropism (-45º). The mycelium grew from the bottom of the figure and developed as a conical structure like Figure 13A until the tips exceeded the threshold distance from the mycelium when they were directed back towards each other by the long-range positive autotropism. A closed structure results. |
Figure 15 illustrates the ‘development’ of a simulated mushroom primordium.
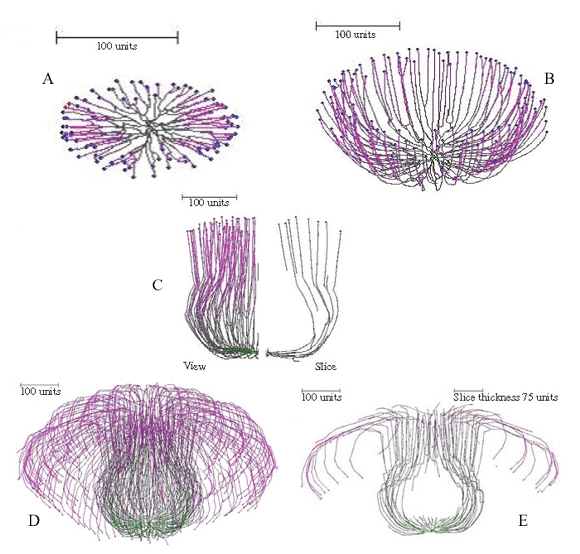 |
Figure 15. Successive stages in ‘development’ of a simulated mushroom primordium. For the first 100 time units a 90º gravitropism was imposed to create a flat colony (Figure 15A); for the next 200 time units a gradual change of plagiogravitropism to a negative gravitropism forms a cup-shape (Figure 15B). Subsequent increase in the impact of the long distance positive autotropism forces the cup to close; and then reduction in impact of this factor restores the vertical growth, forming a bottle-shaped stem (Figure 15C). Later changes of long distance autotropic and (positive) gravitropic parameters cause the community of hyphal tips to cascade down the outside of the stem, forming something resembling a mushroom cap (Figures 15D–E). |
It is noteworthy in these figures, especially the 'developmental sequence' illustrated in Figure 15, that the simulations pass through intermediate shapes that are similar to the fruit bodies of other (non-mushroom) fungi. These include the open more-or-less saucer-shaped or cup-like apothecia of discomycete Ascomycota (Figures 13A–B, 15B), the closed cleistothecial ascoma or hypogeous fruit body (Figure 14), and the perithecial flask-shaped or bottle-like ascoma of pyrenomycete Ascomycota (Figure 15C).
Another simulation of a mushroom primordium is shown in Figure 16.
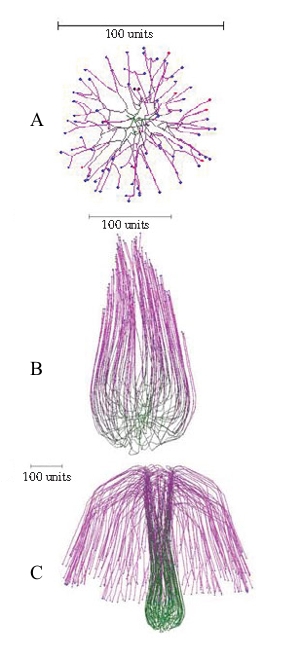 |
| Figure 16.Another simulation of a mushroom primordium. (A) A spherical colony was first grown for 76 time units. (B) This was converted into an organized structure, like the developing mushroom stem, by applying the parallel galvanotropism for 250 time units. (C) Subsequent application of a positive gravitropic reaction (as used in Figure 15D) formed a cap-like structure (1000 time units). Long range autotropism was not used. Parallel tropism and current related positive galvanotropism were set to 0.1 after the age of the developing spherical colony reached 76 time units. Tropism persistence factor was 0.1, hyphal density field hypothesis was used, with a branching threshold of 0.06 field units, field based self-avoidance reaction was used, and the field was generated by all of the mycelium. |
Conclusions
The remarkable reality of the simulations the Neighbour-Sensing program produces encourages confidence in the accuracy and reliability of the Neighbour-Sensing mathematical model on which it is based, and this confidence extends to the various enhancements that have been outlined above. That confidence leads us to believe that the model is revealing hidden facts about the behaviour of live fungi.
Consequently, it is our belief that the experiments described above have exposed a fascinating feature of the ‘crowd behaviour’ of fungal hyphal tips, which is that the shapes of complex fungal fruit bodies can be simulated by applying the same regulatory functions to every one of the growth points active in a structure at any specific time.
All parameter sets that generate shapes reminiscent of fungal fruit bodies feature a sequence of changes in parameter settings that are applied to all hyphal tips in the simulation. No localized regulation is necessary. No global control of fruit body geometry is necessary. The shape of the fruit body emerges from the concerted response of the entire population of hyphal tips, in the same way, to the same signals. This is the most significant observation of this series of modelling experiments.
In the real biological system, such morphogenetic programmes could be based on internal ‘clocks’ of some sort that synchronise behaviour across a developing structure based on time elapsed since some initiating event.
Absence of global control of fruit body geometry does not necessarily imply an absence of localised control of details of fruit body structure. Indeed, by its very nature, the ‘sensing of neighbouring hyphae’ aspects of the model would support the interpretation of ‘Reijnders’ hyphal knots’ [see section 12.16 of our 21st Century Guidebook to Fungi] as a central ‘inducer’ hypha organising differentiation of a small group of surrounding hyphae to regulate detailed structures within fruit body tissues.
Overall, therefore, we believe the Neighbour-Sensing model to be a true representation of the growth patterns of live fungi; but it is not yet perfect. A feature that remains to be implemented in the model is hyphal fusion (or hyphal anastomosis), which is such an important feature of living mycelia [see section 5.17 of our 21st Century Guidebook to Fungi].
Initial work on the mathematics of this suggests that hyphal fusion can be catered for in the algorithms underlying the Neighbour-Sensing model. Inclusion of anastomosis would enable the model to generate biologically inspired networks and so provide a tool to analyse these networks to yield information about connectivity, minimum path length, etc. In addition, it would be possible to address network robustness in silico by investigating the effect of removal of network links on connectivity.
Looking further into the future, it should be possible to add physiological data, such as substrate uptake and substrate transport kinetics, to growth and branching. Since the Neighbour-Sensing model ‘grows’ a realistic mycelium and tracks all of the hyphal segments so generated, there is no mathematical impediment to assigning to those hyphal segments the algebraic characteristics defined to describe substrate uptake, utilization and translocation kinetics, and their variation with age of the hyphal section.
The computation load would be extremely large; nevertheless, the ultimate model could be something akin to computer models of Earth’s atmosphere and be able not only to simulate the growth of a mycelium, but also to plot its use of substrates, and its accumulation, translocation and redistribution of resources within its structure.
Among more immediate prospects for further development (and they are still only prospects at this time) are cyberspecies and improved understanding of hyphal and mycelial evolution.
The opportunity to tailor parameter sets (or ‘strategies’) to simulate specific species of fungi (the individual parameter sets being our cyberspecies) became evident in our first experiments with the model in which distinctions could be made between cybermycelia with morphological similarities to the Boletus, Amanita and Tricholoma types of young mycelia published by Nils Fries [view now]. Comparable microscopic observations of young mycelia of any live fungus should enable the derivation of parameter sets that produce cybermycelia which are exact simulations of the living material. The hope would be that a sufficiently wide panel of such cyberspecies could identify which aspects of hyphal growth and branching enable taxonomic ranks (genera, families, classes) to be distinguished.
This may also contribute to understanding hyphal and mycelial evolution because we might imagine that the evolutionary origins of particular aspects of the kinetics of hyphal growth and branching could be revealed by comparison of cyberspecies representing living taxa with known evolutionary relationships. The way the evolution of the fungal hyphal 'lifestyle' might have been woven into the evolution of life on planet Earth, is dealt with in our recent book Fungal Biology in the Origin and Emergence of Life [Amazon page].
Copyright © David Moore 2017