4.9 Growth kinetics
So far we have described the basic kinetics of mycelial growth in words. Converting them to algebra results in the relationships we illustrated in Figs 7-9 being expressed in the equation:
Ē = µmax G
where Ē is the mean extension rate of the colony margin;
µmax is the maximum specific (biomass) growth rate;
and G is the hyphal growth unit length.
As can be seen from Fig. 13 and Table 2 , the factors which determine the radial growth rate of the colony (Kr) are the specific growth rate of the fungus (μ) and the width of the peripheral growth zone (w); that is, Kr = wμ.
The fungal colony therefore grows outward radially at a linear rate (that is, an arithmetic plot of colony radius against time forms a straight line), continually growing into unexploited substratum. As it does so, the production of new branches ensures the efficient colonisation and utilisation of the substratum. For the colony as a whole, the peripheral growth zone is a ring of active tissue at the colony margin which is responsible for expansion of the colony. At the level of the individual hypha, the peripheral growth zone corresponds to the volume of hypha contributing to extension growth of the apex of that hypha (the hyphal growth unit).
The rate of change in conditions below a colony will be related to the density (biomass per unit surface area) of the fungal biomass supported. It follows from this that a profusely branching mycelium (low value of G) will develop unfavourable conditions in the medium below the colony more rapidly than a sparsely branching mycelium (high value of G). Consequently, a relationship between G and w would be anticipated, and is observed. It means, for example, that Kr can be used to study the effect of temperature on fungal growth because w is not affected appreciably by temperature, however the concentration of glucose (for example) does affect w, so Kr cannot be used to investigate the effect of nutrient concentration. The biological consequence of this is that filamentous fungi can maintain maximal radial growth rate over nutrient-depleted substrates.
Unlike colonies formed by unicellular bacteria and yeasts, where colony expansion is the result of the production of daughter cells and occurs only slowly, the ability of filamentous fungi to direct all their growth capacity to the hyphal apex allows the colony to expand far more rapidly. Importantly, the fungal colony expands at a rate which exceeds the rate of diffusion of nutrients from the surrounding substratum.
Although nutrients under the colony are rapidly exhausted, the hyphae at the edge of the colony have only a minor effect on the substrate concentration and continue to grow outwards, exploring for more nutrients. In contrast, the rate of expansion of bacterial and yeast colonies is extremely slow and less than the rate of diffusion of nutrients (Table 3). Colonies of unicellular organisms quickly become diffusion limited and therefore, unlike fungal colonies, can only attain a finite size.
| Table 3. Colony radial growth rate (Kr) of bacterial and fungal colonies cultivated at their optimum temperatures | |||
| Species | w (μm) |
μ (h-1) |
Kr (μmh-1) |
| Bacteria | |||
| Escherichia coli | 91 |
0.28 |
18 |
Streptococcus faecalis |
Not done |
0.65 |
18 |
Pseudomonas florescens |
Not done |
0.59 |
29 |
Myxococcus xanthus (non-motile) |
Not done |
Not done |
20 |
Streptomyces coelicolor |
Not done |
0.32 |
22 |
| Fungi | |||
Candida albicans (mycelial form) |
119 |
0.39 |
46 |
| Penicillium chrysogenum | 496 |
0.16 |
76 |
| Neurospora crassa | 6800 |
0.26 |
2152 |
| Data summarised from Oliver & Trinci, 1985. | |||
We have discussed how hyphal extension growth follows a few general relationships that are conveyed in relatively simple equations (above and Section 4.4); so, it follows that hyphal growth kinetics are well suited to mathematical modelling, using these word-equations:
- Ē, the mean tip extension rate, is given by µmax (the maximum specific growth rate) multiplied by G, the hyphal growth unit.
- G is defined as the average length of a hypha supporting a growing tip.
- G, consequently, is given by Lt, total mycelial length, divided by Nt, the total number of tips.
In a fungal colony, the hyphal growth unit is approximately equal to the width of the peripheral growth zone, which is a ring-shaped peripheral area of the mycelium that contributes to radial expansion of the colony.
- In a mycelium that is exploring the substrate, branching will be rare and so G will be large. G is therefore an indicator of branching density.
- A new branch is initiated when the capacity for a hypha to extend increases above Ē, thereby regulating G to a uniform value indicative of the characteristic branching density of that fungus under those growing conditions.
All these features of normal filamentous hyphal growth can be expressed algebraically in a vector-based mathematical model in which the growth vector of each virtual hyphal tip is calculated at each iteration of the algorithm by reference to the surrounding virtual mycelium. For example, the Neighbour-Sensing computer program starts with a single hyphal tip, equivalent to a fungal spore. Each time the program runs through its algorithm the tip advances by a growth vector (initially set by the user) and may branch (with an initial probability set by the user).
In the Neighbour-Sensing program each hyphal tip is an active agent, described by its three-dimensional position in space, length, and growth vector, that can vector within three-dimensional data space using rules of exploration that are set (initially by the experimenter) within the program. The rules are biological characteristics such as:
- the basic kinetics of in vivo hyphal growth,
- branching characteristics (frequency, angle, position),
- tropic field settings that involve interaction with the environment.
The experimenter can alter parameters to investigate their effect on form; the final geometry is reached by the program (not the experimenter) adapting the biological characteristics of the active agents during their growth, as in life. This is called the Neighbour-Sensing model and it brings together the essentials of hyphal growth kinetics into mathematical cyberfungus that can be used for experimentation on the theoretical rules governing hyphal patterning and tissue morphogenesis (Meškauskas et al., 2004 a & b).
The Neighbour-Sensing model ‘grows’ a simulated cybermycelium using realistic branching rules decided by the user. As the cyberhyphal tips grow out into the modelling space the model tracks where they have been, and those tracks become the hyphal threads of the cybermycelium. All positioning information is stored by the model as numerical data and so the data handling work becomes more and more extensive as branching produces more hyphal tips and the cybermycelium ‘grows’ in three dimensions on the computer monitor; it is this steady growth process that generates the very large amount of data.
The process of simulation is programmed as a closed loop. This loop is performed for each currently existing hyphal tip of the mycelium and the algorithm:
- Finds the number of neighbouring segments of mycelium (N). A segment is counted as neighbouring if it is closer than the given critical distance (R). In the simplest case we did not use the concept of the density field, preferring a more general formulation about the number of the neighbouring tips.
- If N<Nbranch (the given number of neighbours required to suppress branching), there is a certain given probability (Pbranch) that the tip will branch. If the generated random number (0...1) is less than this probability, the new branch is created, and the branching angle takes a random value. The location of the new tip initially coincides with the current tip. This stochastic branch generation model is similar overall to earlier ones in which distance between branches and branching angles followed experimentally measured statistical distributions.
Initial versions of the model did not implement tropic reactions (to test the kind of morphogenesis that might arise without this component). Later versions of the model tested how autotropic reactions affected the simulation. This model is predictive and successfully describes the growth of hyphae, so confirming its credibility and indicating plausible links between the equations and real physiology; but it is just one of several mathematical models of fungal growth that have been published over the past thirty years. For a wider view of this research we refer you (in alphabetical order) to Bartnicki-Garcia et al. (1989), Boswell et al. (2003), Boswell (2008), Davidson (2007), Du et al. (2019), Goriely & Tabor (2008), Moore et al. (2006), Moore & Meškauskas (2017), Prosser (1990, 1995a & b), Vidal-Diez de Ulzurrun et al. (2015) and Wang et al. (2019). Because fungi vary enormously in size, from single-celled microscopic organisms to some of the largest organisms living on earth, Aguilar-Trigueros et al. (2017) applied allometry to fungi, claiming that scaling fungal traits to body size could yield valuable information about the ecology and functioning of those species.
Most models published so far simulate growth of mycelia on a two-dimensional plane; the Neighbour-Sensing model, however, whilst being as simple as possible, is able to simulate formation of a spherical, uniformly dense fungal colony in a visualisation in three-dimensional space. A description of the mathematics on which the model is based can be found in Moore et al. (2006); we will not dwell on this aspect here. The complete application can be downloaded for personal experimentation elsewhere on our host website [at this URL: http://www.davidmoore.org.uk/CyberWEB/index.htm].
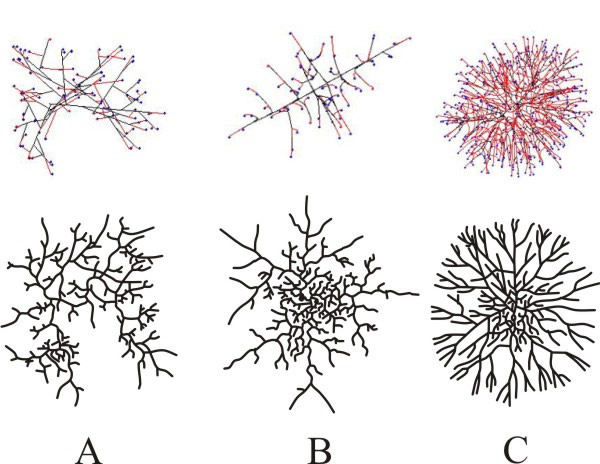
The Neighbour-Sensing model successfully imitates the three branching strategies of fungal mycelia illustrated by Nils Fries in 1943 (Fig. 16 compares computer simulations with the original 1943 illustrations shown previously in Figs 3 to 5).
|
| Fig. 16. Simulation of the three different colony types described by Fries (1943). Panel A shows the Boletus type, B the Amanita type and C the Tricholoma type. The modelling parameters used for each of these simulations are described in the text. The simulation is the upper figure in each case. |
The Neighbour-Sensing model shows that random growth and branching (i.e. a model that does not include the local hyphal tip density field effect or any other tropism) is sufficient to form a spherical colony. The colony formed by such a model is more densely branched in the centre and sparser at the border; a feature observed in living mycelia. Models incorporating local hyphal tip density field to affect patterning produced the most regular spherical colonies. As with the random growth models, making branching sensitive to the number of neighbouring tips forms a colony in which a near uniformly dense, essentially spherical, core is surrounded by a thin layer of slightly less dense mycelia.
Using the branching types discussed by Fries (1943) as a comparison, the morphology of virtual colonies produced when branching (but not growth vector) was made sensitive to the number of neighbouring tips was closest to the so-called Boletus type (Fig 16A). This suggests that the Boletus type branching strategy does not use tropic reactions to determine patterning, nor some pre-defined branching algorithm. Evidently, hyphal tropisms are not always required to explain ‘circular’ mycelia (that is, mycelia that are spherical in three-dimensions).
When the Neighbour-Sensing model implements the negative autotropism of hyphae, a spherical, near uniformly dense colony is also formed, but the structure differs from the previously mentioned Boletus type, being more similar to the Amanita rubescens type, characterised by a certain degree of differentiation between hyphae (Fig. 16B):
- first rank hyphae tending to grow away from the centre of the colony;
- second rank hyphae growing less regularly and filling the remaining space.
In the early stages of development such a colony is more star-like than spherical. It is worth emphasising that this remarkable differentiation of hyphae emerges in the visualisation even though all virtual hyphae are driven by the same algorithm. The program does not include routines implementing differences in hyphal behaviour.
Finally, when both autotropic reaction and branching are regulated by the hyphal density field, a spherical, uniformly dense colony is also formed. However, the structure is different again, such a colony being like the Tricholoma type illustrated by Fries (1943) (Fig. 16C). This type has the appearance of a dichotomous branching pattern, but it is not a true dichotomy. Rather the new branch, being very close, generates a strong density field that turns the growth vector of the older tip away from the new branch.
Hence the Amanita rubescens and Tricholoma branching strategies may be based on a negative autotropic reaction of the growing hyphae while the Boletus strategy may be based on the absence of such a reaction, relying only on density-dependent branching. Differences between Amanita and Tricholoma in the way that the growing tip senses its neighbours may be obscured in life. In Amanita and Boletus types, the tip may sense the number of other tips in its immediate surroundings. In the Tricholoma type, the tip may sense all other parts of the mycelium, but the local segments have the greatest impact.
This model shows that the broadly different types of branching observed in the fungal mycelium are likely to be based on differential expression of relatively simple control mechanisms. The ‘rules’ governing branch patterning (that is, the mechanisms causing the patterning) are likely to change in the life of a mycelium, as both intracellular and extracellular conditions alter. Some of these changes can be imitated by making alterations to specific model parameters during a simulation. By switching between parameter sets it is possible to produce more complex structures.
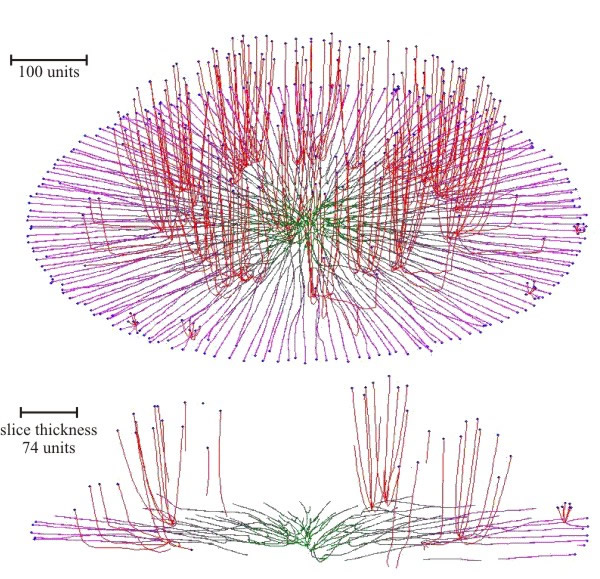
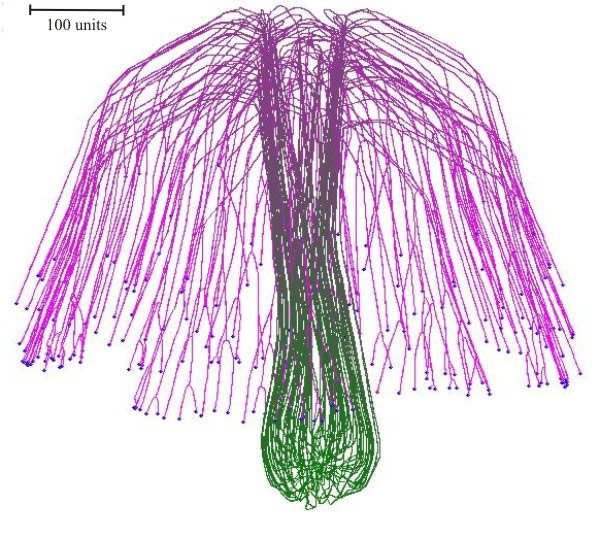
Experiments with the model simulated both colonial growth of the sort that occurs in Petri dish cultures (Fig. 17), and development of a mushroom-shaped ‘fruit body’ (Fig. 18). These experiments make it evident that it is not necessary to impose complex spatial controls over development of the mycelium to achieve specific geometrical forms. Rather, geometrical form of the mycelium emerges because of the operation of specific locally-effective hyphal tip interactions.
|
| Fig. 17. Simulation of colonial growth of the sort that occurs in Petri dish cultures. Oblique view (top) and slice of the colony (bottom), where secondary branching was activated at the 220-time unit. The secondary branches had negative gravitropism. For both primary and secondary branches the growth was simulated assuming negative autotropic reaction and density-dependent branching. If the density allowed branching, the branching probability was 40% per iteration (per time unit). The final age of the colony was 294-time units. Secondary branches are colour-coded red, and hyphae of the primary mycelium are coloured green (oldest) to magenta (youngest), depending on the distance of the hyphal segment from the centre of the colony (modified from Meškauskas et al., 2004b; reproduced with permission from Elsevier). |
|
| Fig. 18. Simulation of a (3-dimensional) mushroom primordium. A spherical colony was first 'grown' for 76-time units. This was converted into an organised structure, like the developing mushroom stem by applying the parallel galvanotropism for 250-time units. Subsequent application of a positive gravitropic reaction formed a cap-like structure (1,000-time units) (modified from Meškauskas et al., 2004a; reproduced with permission from Elsevier). |
These computer simulations suggest that because of the kinetics of hyphal tip growth, very little regulation of cell-to-cell interaction is required to generate the overall architecture of fungal fruit body structures or the basic patterning of the mycelium. Specifically:
- Complex fungal fruit body shapes can be simulated by applying the same regulatory functions to all the growth points active in a structure at any specific time.
- The shape of the fruit body emerges as the entire population of hyphal tips respond together, in the same way, to the same signals.
- No global control of fruit body geometry is necessary (Meškauskas et al., 2004a & b).
The experiments described above have exposed a fascinating feature of the ‘crowd behaviour’ of fungal hyphal tips, which is that the shapes of complex fungal fruit bodies can be simulated by applying the same regulatory functions to every one of the growth points active in a structure at any specific time. All parameter sets that generate shapes reminiscent of fungal fruit bodies feature a sequence of changes in parameter settings that are applied to all hyphal tips in the simulation. No localised regulation is necessary. Absence of global control of fruit body geometry does not necessarily imply an absence of localised control of details of fruit body structure. Indeed, by its very nature, the ‘sensing of neighbouring hyphae’ aspects of the model would support the interpretation of ‘Reijnders’ hyphal knots’ (Reijnders, 1963; and see Chapter 12, especially Section 12.16) as a central ‘inducer’ hypha organising differentiation of a small group of surrounding hyphae to regulate detailed structures within fruit body tissues.
The remarkable reality of the simulations generated by the Neighbour-Sensing program encourages confidence in the accuracy and reliability of the Neighbour-Sensing mathematical model on which it is based. That confidence leads us to believe that the model is revealing unexpected capabilities of the hyphal lifestyle of fungi; but we feel that we have only just scratched the surface of what this mathematical model is able to reveal; the model is not yet perfect. A feature that remains to be implemented in the model is hyphal fusion (or hyphal anastomosis), which is such an important feature of living mycelia (Section 5.16). Initial work on the mathematics of this suggests that hyphal fusion can be catered for in the algorithms underlying the Neighbour-Sensing model. Inclusion of anastomosis would enable the model to generate biologically inspired networks and so provide a tool to analyse these networks to yield information about connectivity, minimum path length, etc. In addition, it would be possible to address network robustness in silico by investigating the effect of removal of network links on connectivity.
Looking further into the future, it should be possible to add physiological data, such as substrate uptake and substrate transport kinetics, to growth and branching. Since the Neighbour-Sensing model ‘grows’ a realistic mycelium and tracks all the hyphal segments so generated, there is no mathematical impediment to assigning to those hyphal segments the algebraic characteristics defined to describe substrate uptake, utilisation and translocation kinetics, and their variation with age of the hyphal section. Recently developed next-generation physiology approaches study microbial communities at the single cell level (Hatzenpichler et al., 2020). If these could be applied to a filamentous fungal hypha, they could furnish the data about how successive compartments behave in normal extension growth and during differentiation, and inform future versions of the Neighbour-Sensing model.
The opportunity to tailor parameter sets (or ‘strategies’) to simulate specific species of fungi (the individual parameter sets being our cyberspecies) became evident in our first experiments with the model in which distinctions could be made between cybermycelia with morphological similarities to the Boletus, Amanita and Tricholoma types of young mycelia discussed above. Comparable microscopic observations of young mycelia of any live fungus should enable the derivation of parameter sets that produce cybermycelia which are exact simulations of the living material. This may also contribute to understanding hyphal and mycelial evolution because we might imagine that the evolutionary origins of specific aspects of the kinetics of hyphal growth and branching could be revealed by comparison of cyberspecies representing living taxa with known evolutionary relationships.
As an aside, it is also worth noting that mycelium networks are promising candidates for designing unconventional computing devices in which electrical signals propagate and interact, and progress is being made in creating sensing and computational fungal automata with fungal mycelia (Adamatzky, 2018: Goles et al., 2020; Beasley et al., 2021). Electrical activity detected in mycelium of Pleurotus ostreatus is characterised by slow (over hours) waves of baseline potential drift and fast (in minutes) spikes of electrical potential resembling the action potentials associated with the passage of an impulse along the membranes of nerves and muscle cells in animals (Adamatzky & Gandia, 2021); the mycelial electrical activity is even anaesthetised by exposure to chloroform vapour! The way filamentous fungi explore the environment in which their mycelia grow can serve as a metaphor for routing algorithms in mobile (cell phone) communication networks. These seek the most advantageous path between a source and a destination node. An algorithm based on the mycelium metaphor found more advantageous routes and generally performed well in comparison with existing protocols (Wille & Bento, 2021). We wonder what the fungi themselves are thinking about ...
Updated September, 2021